DETERMINANTES
Se llama determinante de una matriz cuadrada a un número que se obtienen operando de cierta forma con los elementos de la matriz.
Si es de orden 2x2
det(A)=
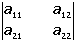 = a 11 a 22 - a 12 a 21
= a 11 a 22 - a 12 a 21
Si es de orden 3x3
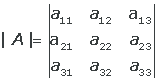
=
= a11 a22 a33 + a12 a23 a 31 + a13 a21 a32 -
- a 13 a22 a31 - a12 a21 a 33 - a11 a23 a32.

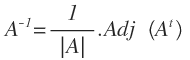





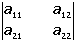 = a 11 a 22 - a 12 a 21
= a 11 a 22 - a 12 a 21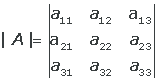 =
=